汉诺塔问题

本文最后更新于：2022年7月31日 晚上

前言

最近两个月一直在看 SICP 的 Youtube 课程，作为一个半路出家的人，自觉基础欠缺，至今已是工作的第四个年头，正如年初计划所言，仅仅依赖于热情去折腾各种简单的玩具已经不再能有效地提升自己了，需要系统化的学习和组织知识。虽然之前也买过实体书，但由于看起来比较难而且也没有风趣的讲解（看的有点枯燥，看完视频后感觉里面的教授真的太有趣了！），所以一直没能看下去（另外一本《算法》也是同样的命运），但幸运的是，Youtube 上有现有的课程，而且还有人做了翻译的字幕，这对吾辈而言真的是方便太多了。汉诺塔是在 SICP 第二课计算过程讲的一个小游戏的例子，由于它真的很有趣，所以吾辈想要写一篇关于它的文章。
那么，为了避免有人还不知道汉诺塔是什么，这里引用一段 wiki 的简介

汉诺塔（港台：河内塔）（Tower of Hanoi）是根据一个传说形成的数学问题：

有三根杆子 A，B，C。A 杆上有 N 个 (N>1) 穿孔圆盘，盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至 C 杆：

每次只能移动一个圆盘；
大盘不能叠在小盘上面。
提示：可将圆盘临时置于 B 杆，也可将从 A 杆移出的圆盘重新移回 A 杆，但都必须遵循上述两条规则。

问：如何移？最少要移动多少次？

简单情况

这里是递归应用最强大的实证

首先来看最简单的情况，将一个初始状态的汉诺塔的所有圆盘移动到另一个柱子上。

课程中给出的解法很有趣

  1. 首先，我们如果需要移动 a(n) 柱子上的圆盘到 b
  2. 如果可以直接移动，则直接移动
  3. 否则，我们可以将之分解为以下 3 步
    1. 移动 a(n-1) 到柱子 c（临时柱）
    2. 然后移动 a(n) 到 b
    3. 最后将 a(n-1) 从移动到 b

然后呢？然后就没有然后了！这个例子真的非常强大，我们使用 4 个圆盘的柱子来演示这一点

下面这个表格是代表操作与状态的变化，如果无法操作，我们将按照上面的规则转换为 3 个子操作，直到可以直接移动为止

操作 a b c
init [1,2,3,4] [] []
a4=>b
--a3=>c
----a2=>b
------a1=>c [2,3,4] [] [1]
------a2=>b [3,4] [2] [1]
------c1=>b [3,4] [1,2]
----a3=>c [4] [1,2] [3]
----b2=>c
------b1=>a [1,4] [2] [3]
------b2=>c [1,4] [] [2,3]
------b1=>c [4] [] [1,2,3]
--a4=>b [] [4] [1,2,3]
--c3=>b
----c2=>a
------c1=>b [] [1,4] [2,3]
------c2=>a [2] [1,4] [3]
------b1=>a [1,2] [4] [3]
----c3=>b [1,2] [3,4] []
----a2=>b
------a1=>c [2] [3,4] [1]
------a2=>b [] [2,3,4] [1]
------c1=>b [] [1,2,3,4] []

可以看到，最终我们成功将圆盘从 a 移动到了 b，这里的关键点是将一个复杂操作分为几步，直到能够执行某些基本操作为止。下面是吾辈使用 ts 实现的最初版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function hanoi(n: number) {
  const res: [from: string, to: string][] = []
  function hanoi(n: number, from: string, to: string, stage: string) {
    if (n === 1) {
      res.push([from, to])
      return
    }
    hanoi(n - 1, from, stage, to)
    hanoi(1, from, to, stage)
    hanoi(n - 1, stage, to, from)
  }

  hanoi(n, 'a', 'b', 'c')
  return res
}

console.log(hanoi(4))

下面则使用更加函数式的风格来完成

改进：实际上汉诺塔是先移动上层的所有圆盘到临时柱，然后移动最下层的圆盘到目标柱，最终将临时圆盘上的所有圆盘移动到目标柱。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function hanoi(n: number) {
  function iter(
    n: number,
    from: string,
    to: string,
    stage: string,
  ): [string, string][] {
    if (n === 1) {
      return [[from, to]]
    }
    return iter(n - 1, from, stage, to)
      .concat(iter(1, from, to, stage))
      .concat(iter(n - 1, stage, to, from))
  }
  return hanoi(n, 'a', 'b', 'c')
}

计算步数

计算步数更加简单，甚至可以写成一个数学函数

$$
f(1)=1 \
f(n)=2f(n-1)+1
$$

如果画成图，就是求一棵树的所有叶子节点

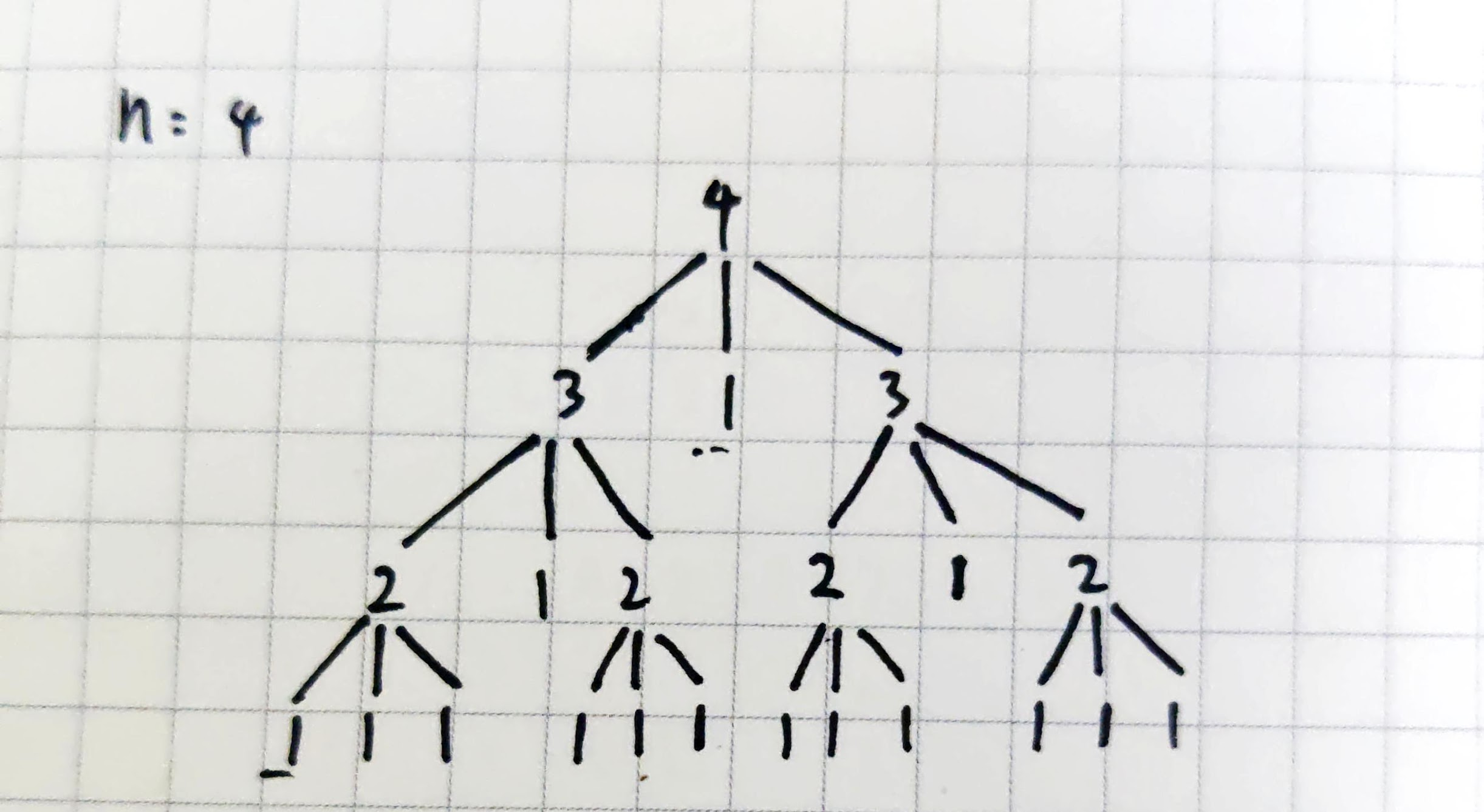
1654526921100

下面使用 ts 非常简单的实现了

1
2
3
4
5
6
7
8
/**
 * 计算移动汉诺塔从 a => b 的步数，本质上公式非常简单
 * @param n
 * @returns
 */
function fn(n: number) {
  return n === 1 ? 1 : fn(n - 1) + fn(1) + fn(n - 1)
}

如果使用缓存，则效率可以高得多

1
2
3
4
5
6
7
const map = new Map<number, number>()
function fn(n: number) {
  if (!map.has(n)) {
    map.set(n, n === 1 ? 1 : fn(n - 1) + fn(1) + fn(n - 1))
  }
  return map.get(n)
}

使用迭代的方式求解

看起来似乎无法使用迭代的方式去解决这个问题，核心是不知道前面还有多少步，或者说没有办法保存当前的移动信息
或许有办法，使用一个对象，通过三个字段的数组保存当前汉诺塔的状态，只要递归函数能智能移动一步，就可以以尾递归（迭代）的方式来解决这个问题，就像人的做法一样，能根据上下文做出合理的移动。

创建一个 HanoiGame 类型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class HanoiGame {
  constructor(public state: { a: number[]; b: number[]; c: number[] }) {}
  check(from: string, to: string) {
    return (
      this.state[from].length !== 0 &&
      (this.state[to].length === 0 || this.get(from) < this.get(to))
    )
  }
  move(from: string, to: string) {
    if (!this.check(from, to)) {
      throw new Error(
        `invalid move ${JSON.stringify(this.state)} ${from} ${to}`,
      )
    }
    this.state[to].unshift(this.state[from].shift())
  }
  get(from: string) {
    return this.state[from][0]
  }
}

const game = new HanoiGame({ a: [1, 2, 3, 4], b: [], c: [] })
const steps = hanoi(4)
steps.forEach((item) => game.move(...item))
console.log(game.state)

初始想法

下面是想到的一种迭代式的非最佳走法

基本思路如下

  1. 从所有操作中过滤出可用的操作，过滤条件为
    • 可移动
    • 上一次移动的不是这个圆盘
  2. 从所有可选操作中选择移动来源与目标差距最小的步骤
  3. 移动它
  4. 记录当前步骤
  5. 传递当前状态进行下一次移动

演示的示例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
function sortBy<T>(arr: T[], fn: (item: T) => number): T[] {
  return [...arr].sort((a, b) => fn(a) - fn(b))
}

function fn(n: number) {
  const game = new HanoiGame({
    a: Array(n)
      .fill(0)
      .map((_, i) => i + 1),
    b: [],
    c: [],
  })
  const res: [string, string][] = []
  function f(game: HanoiGame, last: number) {
    if (
      game.state.a.length === 0 &&
      (game.state.b.length === 0 || game.state.c.length === 0)
    ) {
      return
    }
    const steps = (
      [
        ['a', 'b'],
        ['a', 'c'],
        ['c', 'b'],
        ['b', 'c'],
        ['b', 'a'],
        ['c', 'a'],
      ] as [string, string][]
    ).filter(
      ([from, to]) => game.check(from, to) && game.state[from][0] !== last,
    )
    const list = sortBy(steps, (item) =>
      Math.abs(game.state[item[0]][0] ?? 0 - game.state[item[1]][0] ?? 0),
    )
    const step = list[0]
    res.push(step)
    game.move(...list[0])
    f(game, game.state[step[1]][0])
  }
  f(game, 0)
  return res
}

console.log(fn(1).length)
console.log(fn(2).length)
console.log(fn(3).length)
console.log(fn(4).length)
console.log(fn(5).length)
console.log(fn(6).length)

这个实现有 bug，当 n = 10 时，会无限递归调用导致堆栈溢出

一些观察到的规律

  • 如果按照最佳走法，那么第一步和汉诺塔的层级决定了最终的 target。具体规则是 n % 2 = 0, target != first step to; n % 2 =1, target = first step to

使用迭代的方式计算步数

换个思路求解步数也可以简化为尾递归的形式

1
2
3
4
5
6
function hanoiCountByIter(n: number): number {
  function f(i: number, n: number, sum: number) {
    return i > n ? sum : f(i + 1, n, sum * 2 + 1)
  }
  return f(1, n, 0)
}

使用迭代的方式计算移动步骤

下面是一个迭代实现，基本思路

  • 基本操作，不需要临时柱的操作
  • 复合操作，需要临时柱的操作，一般而言是需要移动两个以上的圆盘的操作
  • 使用链表保存所有的操作，每次递归调用时，都替换其中一个复合操作为 3 个基本操作，并且修改当前操作为要替换的 3 个操作的第一个，直到遇到基本操作
  • 如果还有下一个操作，则继续处理，否则终止迭代
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
interface LinkNode<T> {
  prev?: LinkNode<T>
  next?: LinkNode<T>
  value: T
}

class LinkedList<T> {
  first: LinkNode<T>
  constructor(first: T) {
    this.first = { value: first }
  }
  replace(old: LinkNode<T>, _nodes: T[]) {
    const nodes: LinkNode<T>[] = _nodes.map((value) => ({ value }))
    nodes.forEach((item, i) => {
      item.next = nodes[i + 1]
      item.prev = nodes[i - 1]
    })
    nodes[0].prev = old.prev
    if (old.prev) {
      old.prev.next = nodes[0]
    } else {
      this.first = nodes[0]
    }

    const last = nodes[nodes.length - 1]
    last.next = old.next
    if (old.next) {
      old.prev = last
    }
    return nodes[0]
  }

  *[Symbol.iterator]() {
    let current: LinkNode<T> | undefined = this.first
    while (current) {
      yield current.value
      current = current.next
    }
  }
}

interface HanoiItem {
  value: number
  from: string
  to: string
  stage: string
}

function hanoiForIter(n: number) {
  const list = new LinkedList<HanoiItem>({
    value: n,
    from: 'a',
    to: 'b',
    stage: 'c',
  })
  function f(node: LinkNode<HanoiItem>) {
    const current = node.value
    // 如果可以直接移动，则必须返回
    if (current.value === 1) {
      // 如果没有处理到最后一个节点，则继续处理下一个
      if (node.next) {
        f(node.next)
      }
      return
    }
    // 替换当前复合操作为 3 个子操作
    const newNode = list.replace(node, [
      {
        value: current.value - 1,
        from: current.from,
        to: current.stage,
        stage: current.to,
      },
      {
        value: 1,
        from: current.from,
        to: current.to,
        stage: current.stage,
      },
      {
        value: current.value - 1,
        from: current.stage,
        to: current.to,
        stage: current.from,
      },
    ])
    f(newNode)
  }
  f(list.first)
  return [...list].map((item) => [item.from, item.to] as [string, string])
}

console.log(hanoiForIter(4))

最终，吾辈也是用迭代的方式计算得到了结果（虽然这种方式看起来非常不优雅）

处理任意状态的汉诺塔

以上都在处理从零开始移动汉诺塔，但实际上我们也可以处理任意状态的汉诺塔，以下是吾辈想到的一些处理任意汉诺塔的思路

  1. 优先考虑如何将最大的圆盘移动到合适的位置，必须要考虑无法移动的情况（在无法移动的情况下应该尝试合并两外两个柱子）
  2. 优先移动小的圆盘，合并为连续的便于视为一个复合操作，最终一定能合并到一个柱子上，但不是最优步骤
  3. 穷举所有可能的步骤，得到最佳的走法（或许可以改进为动态规划）– 性能存在问题，无法排除掉大量无效解
  4. 还有一种有趣的方法是算出一个汉诺塔从 0 开始移动到另一个柱子上的所有状态，然后匹配特定状态，进而得到后续所有的步骤 – 复杂度应该是 3*2^n-1，这种方式需要证明一点就是某个状态一定被包含在从初始到结束的所有状态中

本质上汉诺塔的最佳走法可以转换为一棵树，然后按照深度优先的方式遍历获取所有的叶子节点即可。或者以任意方式获取所有的节点及其路径（包含所有 order 的数组），然后排除所有的非叶子节点，最后以 path 排序即可（path 的排序指的是从顶级依次往下比较，有点类似于字符串的左侧优先快速比较）

有什么简单的迭代方式去处理树结构么？

2. 优先移动小的圆盘，合并为连续的便于视为一个复合操作，最终一定能合并到一个柱子上，但不是最优步骤

下面是使用第二种方式实现处理任意状态的汉诺塔

这种方式最大的优点是比较简单，因为它可以像处理一个初始的汉诺塔一样处理任意状态的汉诺塔，只需要将一些有序的圆盘移动到另一个柱子上，而不需要考虑另一个柱子的状态。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
/**
 * 处理任意状态下的汉诺塔
 * @param state
 * @returns
 */
function hanoiAny(state: Record<HanoiPos, number[]>): [HanoiPos, HanoiPos][] {
  function findPos(state: Record<HanoiPos, number[]>, value: number): HanoiPos {
    const arr: HanoiPos[] = ['a', 'b', 'c']
    const res = arr.map((i) => state[i][0])
    return arr[res.indexOf(value)]
  }
  function findContinuousCount(arr: number[]): number {
    function f(i: number, last: number): number {
      return arr[i] !== last + 1 ? i : f(i + 1, arr[i])
    }
    return f(1, arr[0])
  }
  function calcSteps(
    n: number,
    from: HanoiPos,
    to: HanoiPos,
    stage: HanoiPos,
  ): [HanoiPos, HanoiPos][] {
    if (n === 1) {
      return [[from, to]]
    }
    return calcSteps(n - 1, from, stage, to)
      .concat(calcSteps(1, from, to, stage))
      .concat(calcSteps(n - 1, stage, to, from))
  }
  function findStage(from: HanoiPos, to: HanoiPos): HanoiPos {
    const arr: HanoiPos[] = ['a', 'b', 'c']
    return arr.find((i) => i !== from && i !== to)!
  }
  function move(
    state: Record<HanoiPos, number[]>,
    n: number,
    from: HanoiPos,
    to: HanoiPos,
    stage: HanoiPos,
  ): Record<HanoiPos, number[]> {
    return {
      [to]: state[from].slice(0, n).concat(state[to]),
      [from]: state[from].slice(n),
      [stage]: state[stage],
    } as Record<HanoiPos, number[]>
  }
  function count(state: Record<HanoiPos, number[]>): number {
    const arr: HanoiPos[] = ['a', 'b', 'c']
    return arr.map((i) => state[i].length).reduce((a, b) => a + b)
  }
  function iter(state: Record<HanoiPos, number[]>): [HanoiPos, HanoiPos][] {
    // 寻找小的连续圆盘
    const from = findPos(state, 1)
    const n = findContinuousCount(state[from])
    // 判断是否到最终状态了
    // 返回所有步骤
    if (n === count(state)) {
      return []
    }
    // 否则移动所有连续的圆盘到另一个柱子
    // 找到移动的目标
    const to = findPos(state, state[from][n - 1] + 1)
    const stage = findStage(from, to)
    // 移动
    return calcSteps(n, from, to, stage).concat(
      iter(move(state, n, from, to, stage)),
    )
  }
  return iter(state)
}

const state = { a: [1, 4], b: [2], c: [3, 5] }
const game = new HanoiGame(state)
const steps = hanoiAny(state)
steps.forEach((item) => game.move(...item))
console.log(game.state) // { a: [], b: [], c: [ 1, 2, 3, 4, 5 ] }

以上方法都是指数增长 2^n-1，或许有某种线性增长的方法？

1
2
3
4
5
6
7
8
9
function hanoiCount(n: number): number {
  return n === 1 ? 1 : hanoiCount(n - 1) * 2 + 1
}

console.log(
  Array(64)
    .fill(0)
    .map((_, i) => hanoiCount(i + 1)),
)

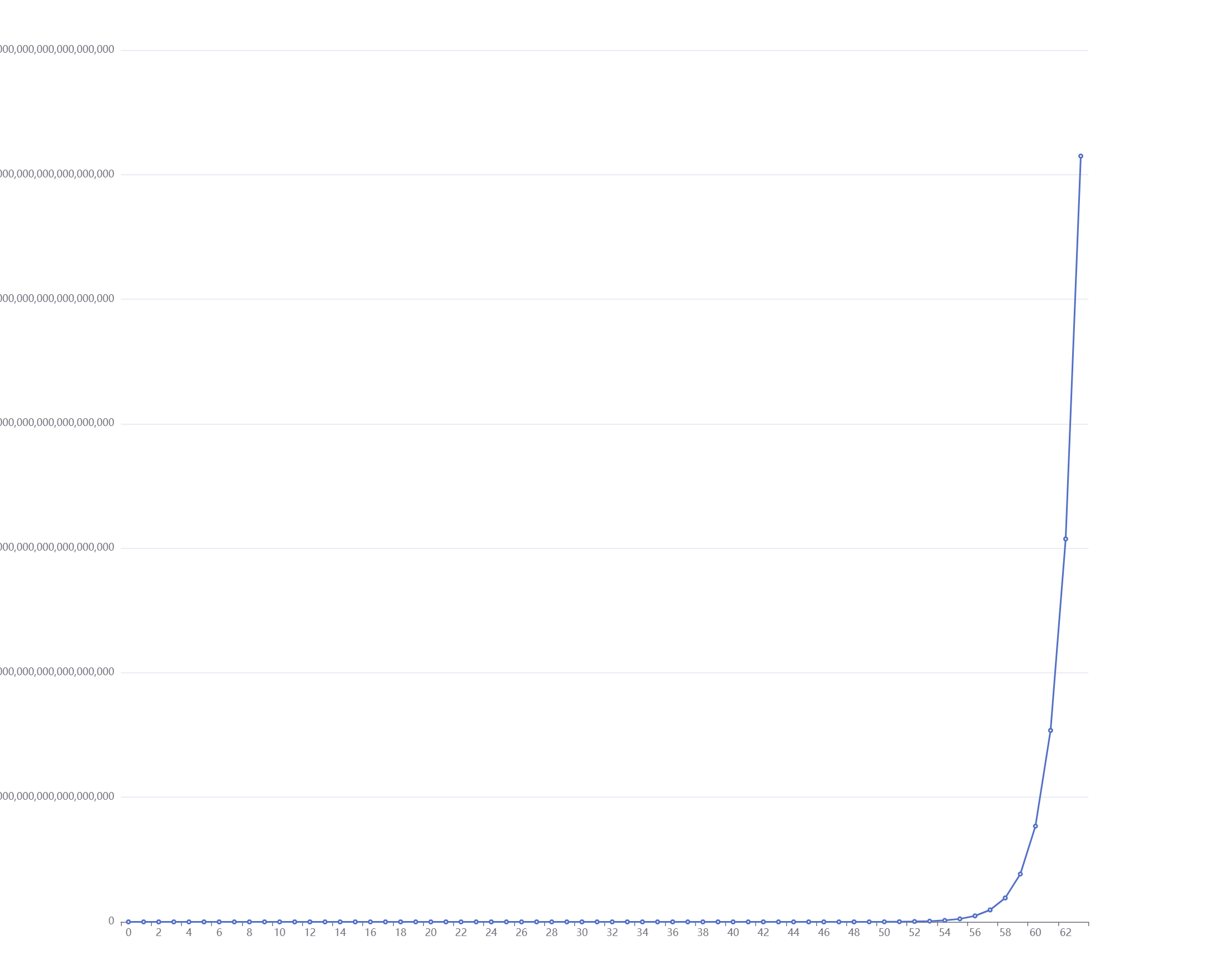
汉诺塔层级-移动次数关系

3. 穷举所有可能的步骤，得到最佳的走法（或许可以改进为动态规划）– 性能存在问题，无法排除掉大量无效解

使用穷举法实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
/**
 * 使用穷举的方式尝试所有可能的走法，找出最优解
 * 深度优先递归的问题是前期会做大量浪费的计算，实际上最优解可能并不在前面，或许应该尝试一下广度优先递归
 * @param state
 * @returns
 */
export function hanoiAnyByReduce(
  state: Record<HanoiPos, number[]>,
): [HanoiPos, HanoiPos][] {
  let min = hanoiAny(state)
  function isComplete(state: Record<HanoiPos, number[]>): boolean {
    return Object.values(state).filter((v) => v.length !== 0).length === 1
  }
  const steps: [HanoiPos, HanoiPos][] = [
    ['a', 'b'],
    ['a', 'c'],
    ['b', 'a'],
    ['b', 'c'],
    ['c', 'a'],
    ['c', 'b'],
  ]
  function calcSteps(
    state: Record<HanoiPos, number[]>,
    prev: [HanoiPos, HanoiPos][],
  ): [HanoiPos, HanoiPos][] {
    const game = new HanoiGame(state)
    return steps.filter((step) => game.check(...step))
  }
  function move(
    state: Record<HanoiPos, number[]>,
    from: HanoiPos,
    to: HanoiPos,
  ): Record<HanoiPos, number[]> {
    return {
      ...state,
      [to]: state[from].slice(0, 1).concat(state[to]),
      [from]: state[from].slice(1),
    }
  }
  function isSuccess(steps: [HanoiPos, HanoiPos][]): boolean {
    if (steps.length < 2) {
      return true
    }
    const last = steps[steps.length - 1]
    const prev = steps[steps.length - 2]
    if (prev[0] === last[1] && prev[1] === last[0]) {
      return false
    }
    return true
  }
  const arr: string[] = []
  function iter(
    state: Record<HanoiPos, number[]>,
    prev: [HanoiPos, HanoiPos][],
  ) {
    // 判断当前是否出现了环
    if (!isSuccess(prev)) {
      return
    }
    const prevString = JSON.stringify(prev)
    arr.push(prevString)
    // 判断当前步数是否已经超过了最佳步数（或者之后可以使用 map 判断相同状态是否已经有更好的走法了）
    if (prev.length >= min.length) {
      return
    }
    if (isComplete(state)) {
      if (prev.length < min.length) {
        min = prev
      }
      return
    }
    // 否则找到所有可行步骤，执行它们
    calcSteps(state, prev).forEach((step) => {
      iter(move(state, ...step), [...prev, step])
    })
  }
  iter(state, [])
  // writeFileSync(path.resolve(__dirname, 'test.json'), JSON.stringify(arr))
  return min
}

1. 优先考虑如何将最大的圆盘移动到合适的位置，必须要考虑无法移动的情况（在无法移动的情况下应该尝试合并两外两个柱子）

使用第一种方法实现，但最终结果和穷举法相同，似乎这就是最优解

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
/**
 * 处理任意状态下的汉诺塔
 * 优先考虑如何将最大的圆盘移动到合适的位置，必须要考虑无法移动的情况（在无法移动的情况下应该尝试合并两外两个柱子）
 */
export function hanoiAnyByDepth(
  state: Record<HanoiPos, number[]>,
  to: HanoiPos,
): [HanoiPos, HanoiPos][] {
  function findPosByNumber(
    state: Record<HanoiPos, number[]>,
    n: number,
  ): HanoiPos {
    return Object.entries(state).find(([_k, v]) =>
      v.includes(n),
    )?.[0] as HanoiPos
  }
  function isMove(
    state: Record<HanoiPos, number[]>,
    from: HanoiPos,
    to: HanoiPos,
    n: number,
  ) {
    const game = new HanoiGame(state)
    return game.get(from) === n && game.check(from, to)
  }
  function move(
    state: Record<HanoiPos, number[]>,
    steps: [HanoiPos, HanoiPos][],
  ): Record<HanoiPos, number[]> {
    const game = new HanoiGame(JSON.parse(JSON.stringify(state)))
    steps.forEach((step) => game.move(...step))
    return game.state
  }
  function findStage(from: HanoiPos, to: HanoiPos): HanoiPos {
    const arr: HanoiPos[] = ['a', 'b', 'c']
    return arr.find((i) => i !== from && i !== to)!
  }
  function iter(
    state: Record<HanoiPos, number[]>,
    from: HanoiPos,
    to: HanoiPos,
    stage: HanoiPos,
    n: number,
  ): [HanoiPos, HanoiPos][] {
    if (from === to) {
      const nextFrom = findPosByNumber(state, n - 1)
      return iter(state, nextFrom, to, findStage(nextFrom, to), n - 1)
    }
    // 移动 from => to 的一个指定值
    // 如果可以直接移动，则直接移动
    if (isMove(state, from, to, n)) {
      return [[from, to]]
    }
    // 否则找到上面影响移动的最大圆盘到临时柱，递归调用该方法
    const values = [...state[from], ...state[to]].sort((a, b) => a - b)
    const nextN = values[values.indexOf(n) - 1]
    const nextForm = findPosByNumber(state, nextN)
    // 应用上面的移动步骤，然后递归调用该方法
    // 移动上面阻碍它移动的圆盘到临时柱
    const before = iter(
      state,
      nextForm,
      stage,
      findStage(nextForm, stage),
      nextN,
    )
    let nextState = move(state, before)
    // 移动当前圆盘
    const current = iter(nextState, from, to, stage, n)
    nextState = move(nextState, current)
    const next = findPosByNumber(nextState, n - 1)
    // 继续下一次迭代移动上面的一个圆盘
    const after = iter(nextState, next, to, findStage(next, to), n - 1)
    return [...before, ...current, ...after]
  }
  const initN = Object.values(state).flat().length
  const initForm = findPosByNumber(state, initN)
  return iter(state, initForm, to, findStage(initForm, to), initN)
}

使用基本的单元测试验证它是有效的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
describe('hanoiAnyByDepth', () => {
  it('basic', () => {
    const state: Record<HanoiPos, number[]> = {
      a: [1, 3, 5],
      b: [],
      c: [2, 4, 6],
    }
    console.log(hanoiAnyByDepth(state, 'c').length)
    console.log(hanoiAny(state).length)
    const game = new HanoiGame(state)
    hanoiAnyByDepth(state, 'b').forEach((step) => game.move(...step))
    expect(game.state['b'].length).toBe(6)
  })
})

大多数情况下，它计算得到的步数要比使用方法 2 得到的步骤少得多，我们可以验证这一点

upset 是一个将汉诺塔状态随机打乱的函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
function findMax(state: Record<HanoiPos, number[]>) {
  const pos: HanoiPos[] = ['a', 'b', 'c']
  return sortBy(
    pos.map((k) => ({
      k,
      v: state[k][state[k].length - 1] ?? 0,
    })),
    (item) => -item.v,
  )[0].k
}
it('findMax', () => {
  console.log(findMax({ a: [1, 3], b: [], c: [2, 4] }))
  console.log(findMax({ a: [1, 2, 3, 4], b: [], c: [] }))
})
it('perf', async () => {
  const list = Array(100)
    .fill(0)
    .map(() => {
      const state = upset(10)
      return {
        first: hanoiAny(state).length,
        second: hanoiAnyByDepth(state, findMax(state)).length,
      }
    })
  await mkdirp(path.resolve(__dirname, '.temp/'))
  await writeJson(path.resolve(__dirname, '.temp/test.json'), [
    {
      name: 'hanoiAny',
      type: 'line',
      data: list.map((item) => item.first),
    },
    {
      name: 'hanoiAnyByDepth',
      type: 'line',
      data: list.map((item) => item.second),
    },
  ])
})

下面是测试用例的结果的可视化图表

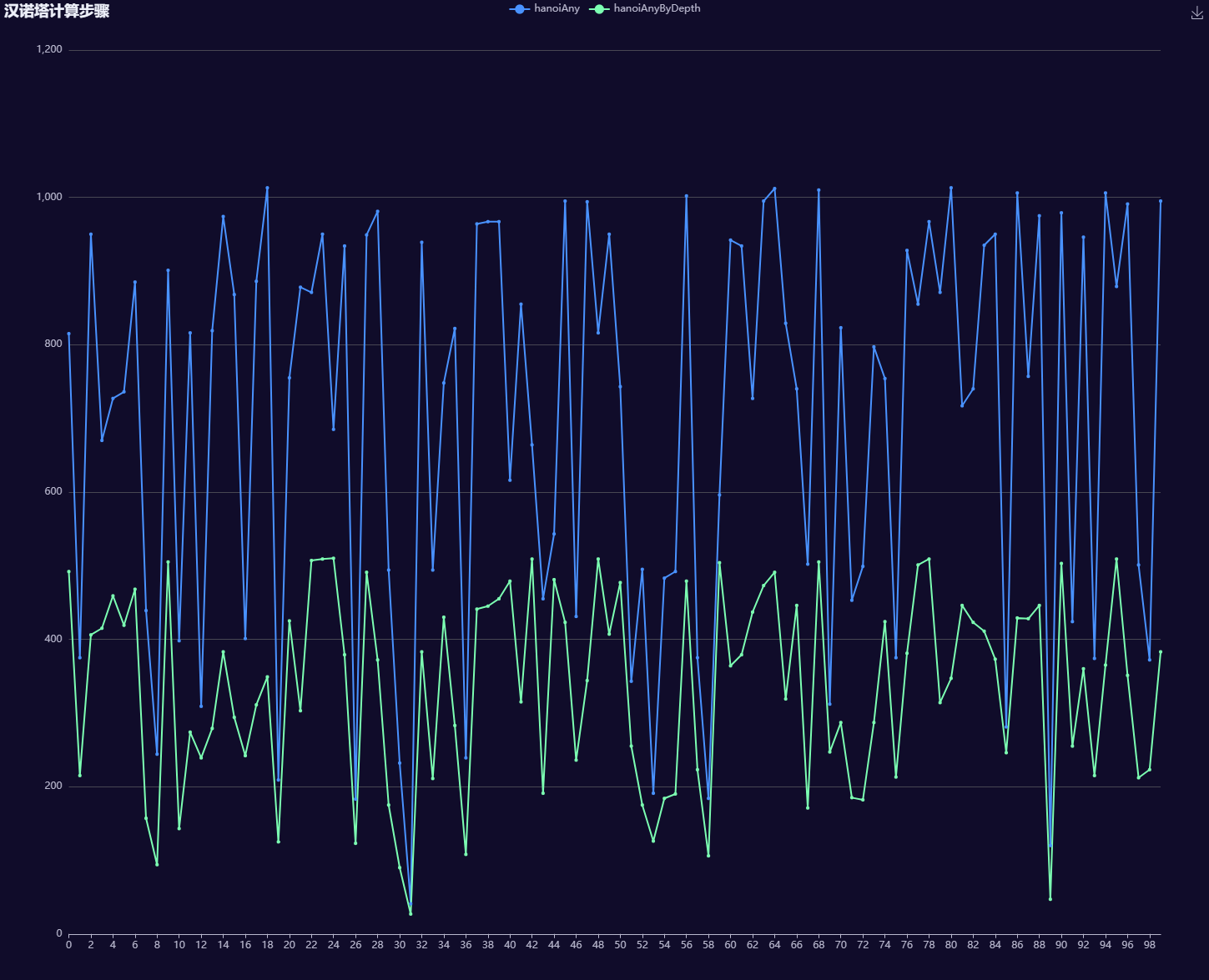
1654530232450

4. 算出一个汉诺塔从 0 开始移动到另一个柱子上最佳步骤的所有状态，然后匹配特定状态，进而得到后续所有的步骤

实际上不可能，事实上可以找到反例，例如以下状态就不会在最佳走法的任意一步状态中

1
2
3
4
5
const state: Record<HanoiPos, number[]> = {
  a: [1, 3],
  b: [],
  c: [2, 4],
}

验证它也很简单

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
function eq(
  a: Record<HanoiPos, number[]>,
  b: Record<HanoiPos, number[]>,
): Record<HanoiPos, HanoiPos> | false {
  const arr: HanoiPos[] = ['a', 'b', 'c']
  const bs = arr.reduce((res, i) => {
    res[JSON.stringify(b[i])] = i
    return res
  }, {} as Record<string, HanoiPos>)
  const res: (HanoiPos | null)[] = arr.map(
    (i) => bs[JSON.stringify(a[i])] ?? null,
  )
  if (res.includes(null)) {
    return false
  }
  return res.reduce((res, v, i) => {
    res[arr[i]] = v!
    return res
  }, {} as Record<HanoiPos, HanoiPos>)
}
it('eq', () => {
  expect(
    eq({ a: [1, 3], b: [2, 4], c: [] }, { a: [1, 3], b: [2, 4], c: [] }),
  ).toBeTruthy()
  expect(
    eq({ a: [1, 3], b: [2, 4], c: [] }, { a: [], b: [2, 4], c: [1, 3] }),
  ).toBeTruthy()
  expect(
    eq({ a: [1, 3], b: [2, 4], c: [] }, { a: [2, 4], b: [], c: [1, 3] }),
  ).toBeTruthy()
  expect(
    eq({ a: [1, 3], b: [2, 4], c: [] }, { a: [2], b: [], c: [1, 3] }),
  ).toBeFalsy()
})
it('hanoiByStream', () => {
  const state: Record<HanoiPos, number[]> = {
    a: [1, 3],
    b: [],
    c: [2, 4],
  }
  const game = new HanoiGame({
    a: [1, 2, 3, 4],
    b: [],
    c: [],
  })
  const i = hanoi(4).findIndex((step) => {
    const res = eq(game.state, state)
    game.move(...step)
    return res
  })
  console.log(i)
})

结语

吾辈最终也实现了一个汉诺塔的在线小游戏，参考：https://rxliuli.github.io/hanoi/

后续还会写几篇吾辈觉得有意思的技术点，包括 cons 如何无中生有的构造数据结构、流与延迟计算、lisp 的解释器和运行时等。

其他 > SICP
#算法
汉诺塔问题
https://blog.rxliuli.com/p/9751355186fd4c5bbad0d041fe85c256/
作者
rxliuli
发布于
2022年4月25日
许可协议