本文最后更新于:2022年6月9日 下午
前言
lisp 中有一种有趣的数据结构,Cons,它使用函数闭包封装了一个两元组的数据结构,并在此之上构建出其他需要的任何数据结构。在此之前,虽然也知道闭包之类的概念,写过一些高阶函数,但并未想过可以使用函数来构建数据结构,下面吾辈会说明如何在 ts 完成。
lisp cons 的 wiki
基本定义如下
$$
c=cons(a,b)\
car(c)=a\
cdr(c)=b
$$
初始实现
cons 初始实现很简单,只需要几行代码即可实现。可以看到,仅仅是使用闭包绑定了参数 a 和 b,并在函数执行时返回它们。
1
2
3
4
5
6
7
8
9
| function cons(a: number, b: number): (n: number) => number {
return (n: number) => (n === 0 ? a : b)
}
function car(cons: (n: number) => number) {
return cons(0)
}
function cdr(cons: (n: number) => number) {
return cons(1)
}
|
可以按照以下方式来使用它
1
2
3
| const n = cons(1, 2)
console.log(car(n))
console.log(cdr(n))
|
为了让它看起来更实用一点,首先使用泛型补充它的类型
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| export interface Cons<A, B> {
(s: 0): A
(s: 1): B
_0: A
_1: B
}
export function cons<A, B>(a: A, b: B): Cons<A, B> {
return ((s: 0 | 1) => (s === 0 ? a : b)) as any
}
export function car<T extends Cons<any, any>>(cons: T): T['_0'] {
return cons(0)
}
export function cdr<T extends Cons<any, any>>(cons: T): T['_1'] {
return cons(1)
}
|
使用以下单元测试验证它
1
2
3
4
5
| it('cons', () => {
const c = cons('hello', 1)
expect(car(c) as string).toBe('hello')
expect(cdr(c) as number).toBe(1)
})
|
看起来没什么了不起的,但下面会使用它(最简单的二元结构)组合成链表和树等更复杂的数据结构。
链表
事实上,只要有了一个二元组,就可以继续组合任意需要的数据结构,链表是一种简单的示例。
这里将 cons 的 car 部分存储链表中当前结点的值,cdr 则存储着指向下一个节点的指针。
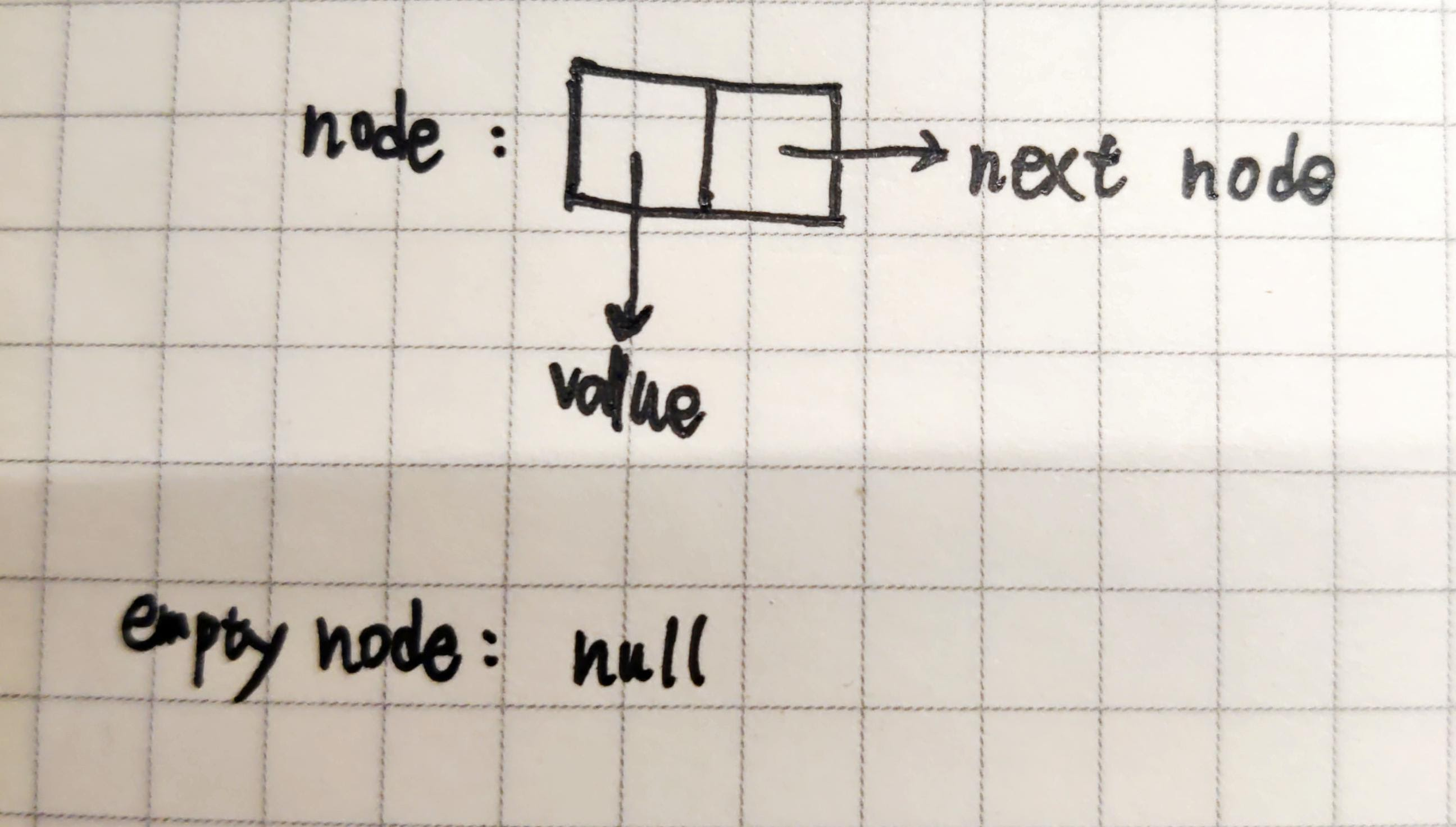
1
2
3
4
5
6
7
8
9
| type List<T> = Cons<T, List<T>> | null
function list(): null
function list<T>(...args: T[]): Exclude<List<T>, null>
function list<T>(...args: T[]): List<T> {
function iter(i: number): List<T> {
return i === args.length ? null : cons(args[i], iter(i + 1))
}
return iter(0)
}
|
下面是一个存储 4 个元素的链表
它会是一个 cons 嵌套调用的过程
1
| cons(1, cons(2, cons(3, cons(4, null))))
|
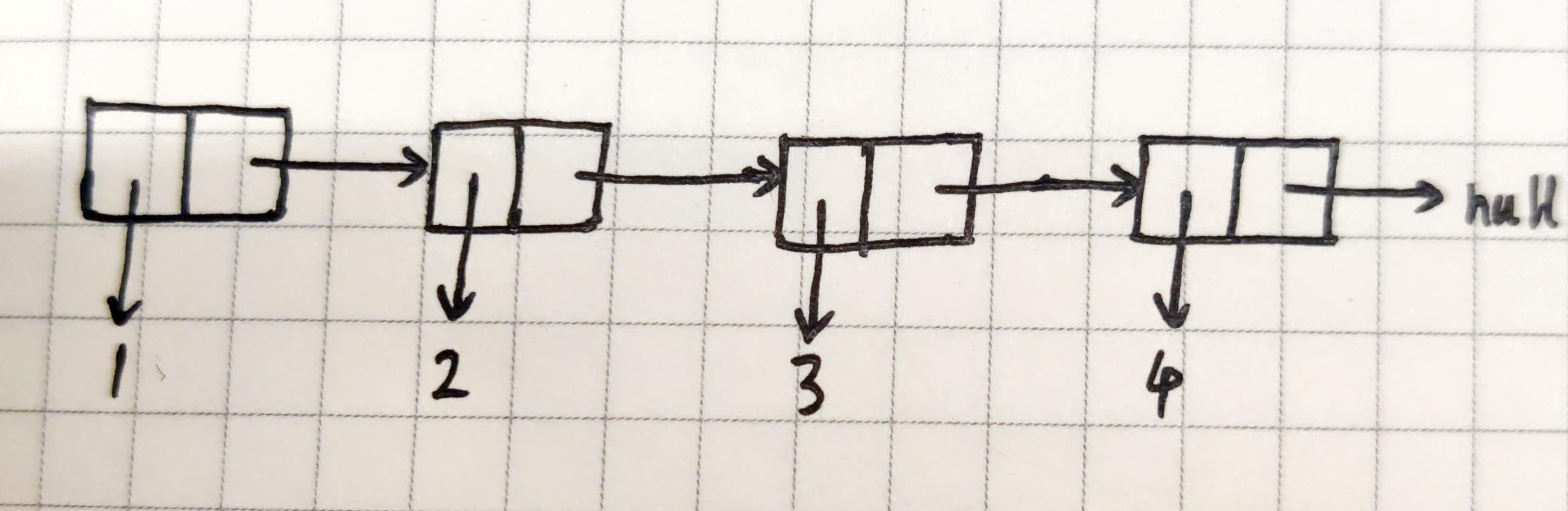
可以为之编写 map/filter/reduce 函数
map/filter 没什么复杂的,只是递归处理每个节点
1
2
3
4
5
6
7
8
9
10
| function map<T, R>(list: List<T>, f: (i: T) => R): List<R> {
return list === null ? null : (cons(f(car(list)), map(cdr(list)!, f)) as any)
}
function filter<T>(list: List<T>, f: (i: T) => boolean): List<T> {
return list === null
? null
: f(car(list))
? cons(car(list), filter(cdr(list), f))
: filter(cdr(list), f)
}
|
下面使用 map 处理的示意图
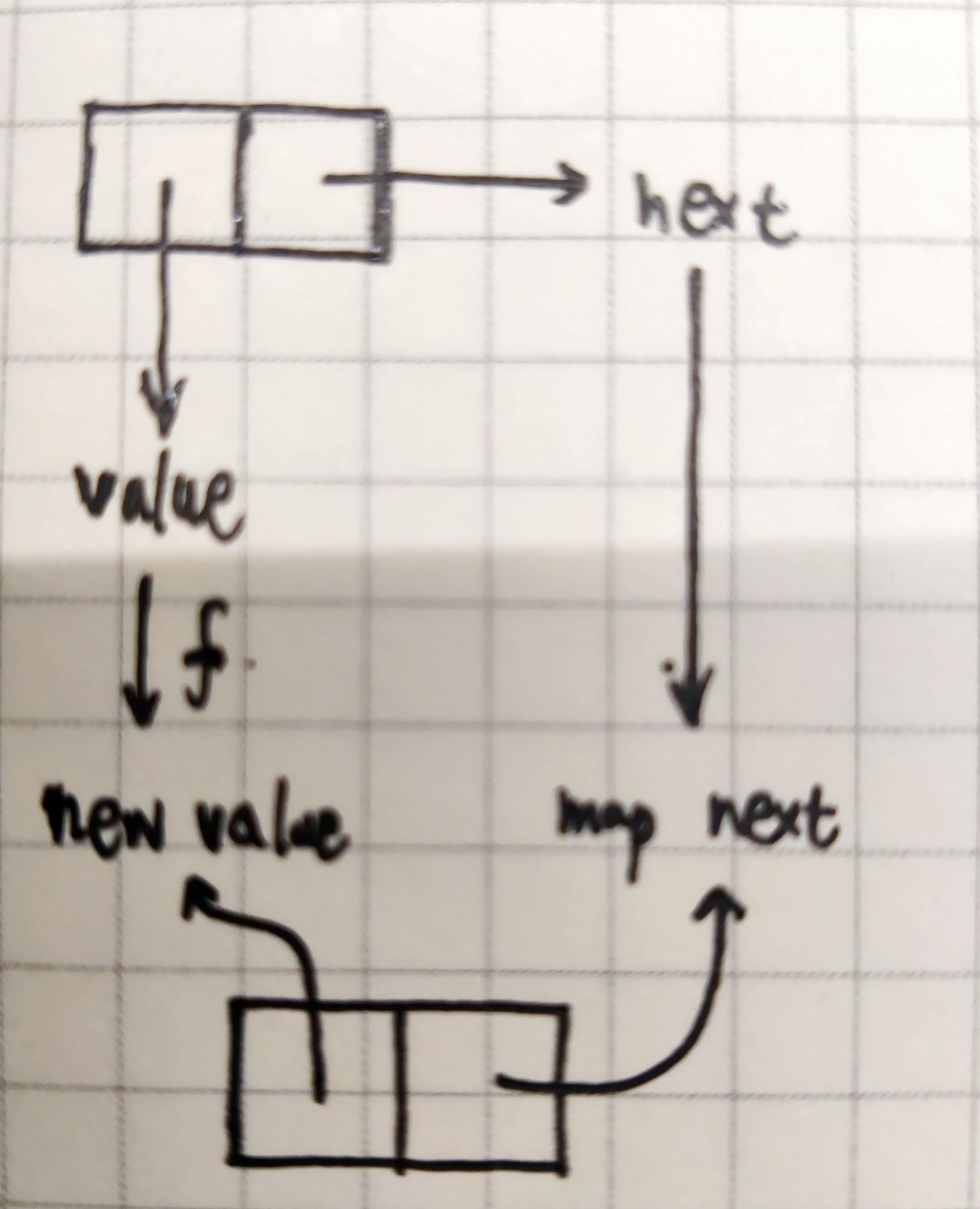
reduce 会有一点特殊,它是一个迭代式的递归
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| function reduce<T>(list: List<T>, f: (res: T, v: T, i: number) => T): T
function reduce<T, R>(
list: List<T>,
f: (res: R, v: T, i: number) => R,
init: R,
): R
function reduce<T, R>(
list: List<T>,
f: (res: R, v: T, i: number) => R,
init?: R,
): R {
function iter(list: List<T>, init: R, i: number): R {
return list === null ? init : iter(cdr(list)!, f(init, car(list), i), i + 1)
}
return init !== undefined
? iter(list, init, 0)
: iter(cdr(list!), car(list!) as unknown as R, 1)
}
|
可以使用以下方式来使用它
1
2
3
4
5
6
7
8
9
| const res = reduce(
map(
filter(list(1, 2, 3, 4), (i) => i % 2 === 0),
(i) => i * 2,
),
(a, b) => a + b,
0,
)
console.log(res)
|
理论上,应该很容易将 map/filter 转换为基于 reduce 的高阶函数,例如下面这段代码是在 js 中基于 reduce 实现 map/filter
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| function map<T, R>(list: T[], f: (i: T) => R): R[] {
return list.reduce((res, i) => {
res.push(f(i))
return res
}, [] as R[])
}
function filter<T>(list: T[], f: (i: T) => boolean): T[] {
return list.reduce((res, i) => {
if (f(i)) {
res.push(i)
}
return res
}, [] as T[])
}
|
如果希望将这里链表的 map/filter 基于 reduce 实现,则目前是不可能的。请注意,上面的代码使用了 push,这是一个修改操作,在函数式编程中更推荐不可变状态。那么,是否有某种方式即不改变状态也能做到呢?吾辈将尝试实现它。
1
2
3
4
5
6
7
8
9
10
11
12
13
| function concat<T>(a: List<T>, b: List<T>): List<T> {
return a === null ? b : cons(car(a), concat(cdr(a), b))
}
function mapForReduce<T, R>(arr: List<T>, f: (i: T) => R): List<R> {
return reduce(arr, (res, i) => concat(res, list(f(i))), null as List<R>)
}
function filterForReduce<T>(arr: List<T>, f: (i: T) => boolean): List<T> {
return reduce(
arr,
(res, i) => (f(i) ? concat(res, list(i)) : res),
null as List<T>,
)
}
|
当然,或许会有人说:每次迭代一个元素时,都需要连接两个链表,这个效率不是很低么?是的,确实很低,所以可以使用另一种稍微怪异的方法。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| function mapForReduce<T, R>(list: List<T>, f: (i: T) => R): List<R> {
return reduce(
list,
(res, i) => {
return i === null ? res : (next) => res(cons(f(i), next))
},
(r: List<R>) => r,
)(null)
}
function filterForReduce<T>(list: List<T>, f: (i: T) => boolean): List<T> {
return reduce(
list,
(res, i) => (f(i) ? (next) => res(cons(i, next)) : res),
(r: List<T>) => r,
)(null)
}
|
诚然,这种方法看起来不会在每次递归时积累栈,但它也会将 res 这个函数不断包裹,最终在 reduce 结束后传入一个参数一次性全部调用,并未解决根本问题,所以下面实现 setCar/setCdr
支持修改 car/cdr
想要实现 set,其实也就是修改闭包绑定的参数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| export interface Cons<A, B> {
(s: 'car'): A
(s: 'cdr'): B
(s: 'setCar'): (v: A) => void
(s: 'setCdr'): (v: B) => void
_0: A
_1: B
}
export function cons<A, B>(a: A, b: B): Cons<A, B> {
return ((s: string) =>
s === 'car'
? a
: s === 'cdr'
? b
: s === 'setCar'
? (v: A) => (a = v)
: (v: B) => (b = v)) as any
}
export function car<T extends Cons<any, any>>(cons: T): T['_0'] {
return cons('car')
}
export function cdr<T extends Cons<any, any>>(cons: T): T['_1'] {
return cons('cdr')
}
export function setCar<T extends Cons<any, any>>(cons: T, v: T['_0']): void {
return cons('setCar')(v)
}
export function setCdr<T extends Cons<any, any>>(cons: T, v: T['_1']): void {
return cons('setCdr')(v)
}
|
可以使用以下单元测试验证
1
2
3
4
5
6
7
8
9
| it('cons', () => {
const c = cons('hello', 1)
expect(car(c) as string).toBe('hello')
expect(cdr(c) as number).toBe(1)
setCar(c, 'liuli')
setCdr(c, 2)
expect(car(c) as string).toBe('liuli')
expect(cdr(c) as number).toBe(2)
})
|
不过在课程中提出了另一种实现,完全使用高阶函数实现,不在 cons 中使用内部判断。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
| export interface Cons<A, B> {
(m: (a: A, b: B, setA: (a: A) => void, setB: (b: B) => void) => any): any
_0: A
_1: B
}
export function cons<A, B>(a: A, b: B): Cons<A, B> {
return ((
m: (a: A, b: B, setA: (a: A) => void, setB: (b: B) => void) => any,
) =>
m(
a,
b,
(n: A) => (a = n),
(n: B) => (b = n),
)) as any
}
export function car<T extends Cons<any, any>>(cons: T): T['_0'] {
return cons((a) => a)
}
export function cdr<T extends Cons<any, any>>(cons: T): T['_1'] {
return cons((_a, b) => b)
}
export function setCar<T extends Cons<any, any>>(
cons: T,
value: T['_0'],
): void {
cons((_a, _b, setA) => setA(value))
}
export function setCdr<T extends Cons<any, any>>(
cons: T,
value: T['_1'],
): void {
cons((_a, _b, _setA, setB) => setB(value))
}
|
现在,重新实现 mapForReduce/filterForReduce
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| function mapForReduce<T, R>(list: List<T>, f: (i: T) => R): List<R> {
const init = cons(null, null) as unknown as List<R>
reduce(
list,
(curr, i) => {
const next = cons(f(i), null) as List<R>
setCdr(curr!, next)
return next
},
init,
)
return cdr(init!)
}
function filterForReduce<T>(list: List<T>, f: (i: T) => boolean): List<T> {
const init = cons(null, null) as unknown as List<T>
reduce(
list,
(curr, i) => {
if (!f(i)) {
return curr
}
const next = cons(i, null) as List<T>
setCdr(curr!, next)
return next
},
init,
)
return cdr(init!)
}
|
对于代码 mapForReduce(list(1, 2, 3, 4), i => i) 的迭代过程图
| i |
curr |
init |
| 1 |
(null, null) |
(null, null) |
| 2 |
(1, null) |
(null, (1, null)) |
| 3 |
(2, null) |
(null, (1, (2, null))) |
| 4 |
(3, null) |
(null, (1, (2, (3, null)))) |
| return |
|
(null, (1, (2, (3, (4, null))))) |
可以看到,每次都修改上一个节点,并且将当前值使用 cons 构造一个新的节点并作为下一个迭代值,最终遍历完整个列表也就将整个列表复制了一份。
树
既然可以通过 cons 构造链表,也自然可以构造树结构,只要定义一个树结构即可。
一个节点是由一个值和可能存在的子节点组成,所以我们这样定义一个树节点。
1
| cons(value, list(sub1, sub2, ...subN))
|
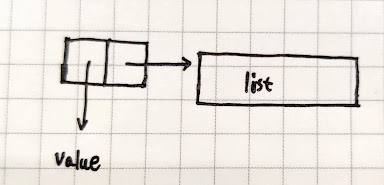
实现非常简单
1
2
3
4
5
6
7
8
| type Tree<T> = Cons<T, List<Tree<T>>>
function tree<T>(value: T, children: List<Tree<T>> = null) {
return cons(value, children)
}
const t = tree(1, list(tree(2, list(tree(3))), tree(4)))
expect(car(t)).toBe(1)
expect(car(car(cdr(t)!))).toBe(2)
|
也可以实现树结构的 map/filter/reduce,可以看到线面的实现都是简单基于 list 的 map/filter 实现。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| function treeReduce<T, R>(tree: Tree<T>, f: (r: R, v: T) => R, init: R): R {
init = f(init, car(tree))
map(cdr(tree), (i) => {
init = treeReduce(i, f, init)
})
return init
}
function treeMap<T, R>(tree: Tree<T>, f: (v: T) => R): Tree<R> {
return cons(
f(car(tree)),
map(cdr(tree)!, (i) => treeMap(i, f)),
)
}
function treeFilter<T>(tree: Tree<T>, f: (v: T) => boolean): Tree<T> | null {
if (!f(car(tree))) {
return null
}
return cons(
car(tree),
filter(
map(cdr(tree)!, (i) => treeFilter(i, f)!),
(i) => i !== null,
),
)
}
|
测试一下
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| const t = tree(1, list(tree(2, list(tree(3))), tree(4)))
it('basic', () => {
expect(car(t)).toBe(1)
expect(car(car(cdr(t)!))).toBe(2)
})
it('treeReduce', () => {
expect(treeReduce(t, (r, i) => [...r, i], [] as number[])).toEqual([
1, 2, 3, 4,
])
})
it('treeMap', () => {
expect(
treeReduce(
treeMap(t, (i) => i * 2),
(r, i) => [...r, i],
[] as number[],
),
).toEqual([1, 2, 3, 4].map((i) => i * 2))
})
it('treeFilter', () => {
const res = treeFilter(t, (i) => i % 2 === 1)
expect(treeReduce(res!, (r, i) => [...r, i], [] as number[])).toEqual([1])
})
|
结语
lisp 是一个看起来很简单的语言,因为似乎一切都是表达式,也不像现代语言一样提供多种构造复合数据的方法(像是 object 对象、struct 结构体、class 类等等)。但这里可以看到,只要支持最简单的复合数据,便可以构造任意复杂的数据结构,一切的复合数据的基石是如此简单以至于难以置信。
事实上,使用 ts 编写一个 lisp 玩具解析器和运行时是如此简单,吾辈会在之后演示它。



